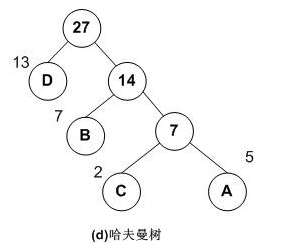
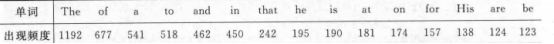1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
| #include <stdio.h>
#include <string.h>
#define N 50
#define M 2 * N-1
typedef struct
{
char data[5];
int weight;
int parent;
int lchild;
int rchild;
}HTNode;
typedef struct
{
char cd[N];
int start;
}HCode;
void CreateHT(HTNode ht[],int n)
{
int i,k,lnode,rnode;
int min1,min2;
for (i=0;i<2*n-1;i++)
ht[i].parent=ht[i].lchild=ht[i].rchild=-1;
for (i=n;i<2*n-1;i++)
{
min1=min2=32767;
lnode = rnode = -1;
for(k=0;k<=i-1;k++)
if(ht[k].parent==-1)
{
if(ht[k].weight<min1)
{
min2=min1;
rnode=lnode;
min1=ht[k].weight;
lnode=k;
}
else if(ht[k].weight<min2)
{
min2=ht[k].weight;
rnode=k;
}
}
ht[lnode].parent=i;
ht[rnode].parent=i;
ht[i].weight=ht[lnode].weight+ht[rnode].weight;
ht[i].lchild=lnode;
ht[i].rchild=rnode;
}
}
void CreateHCode(HTNode ht[],HCode hcd[],int n)
{
int i,f,c;
HCode hc;
for(i=0;i<n;i++)
{
hc.start=n;
c=i;
f=ht[i].parent;
while(f!=-1)
{
if(ht[f].lchild==c)
hc.cd[hc.start--]='0';
else
hc.cd[hc.start--]='1';
c=f;
f=ht[f].parent;
}
hc.start++;
hcd[i]=hc;
}
}
void DispHCode(HTNode ht[],HCode hcd[],int n)
{
int i,k;
int sum=0,m=0,j;
printf("输出哈夫曼编码:\n");
for (i=0;i<n;i++)
{
j=0;
printf(" %s:\t",ht[i].data);
for(k=hcd[i].start;k<=n;k++)
{
printf("%c",hcd[i].cd[k]);
j++;
}
m+=ht[i].weight;
sum+=ht[i].weight * j;
printf("\n");
}
printf("\n平均长度=%g\n",1.0 * sum/m);
}
int main()
{
int n=15,i;
char * str[]={"The","of","a","to","and","in","that","he","is","at","on","for","His","are","be"};
int fnum[]={1192,677,541,518,462,450,242,195,190,181,174,157,138,124,123};
HTNode ht[M];
HCode hcd[N];
for(i=0;i<n;i++)
{
strcpy(ht[i].data,str[i]);
ht[i].weight=fnum[i];
}
CreateHT(ht,n);
CreateHCode(ht,hcd,n);
DispHCode(ht,hcd,n);
return 1;
}
|